Winning strategy
There are two ways to win at roulette and both are based on the science of physics:
- Hope you get an unbalanced wheel and be prepared to exploit this handy fact.
- Base your strategy off of the deterministic nature of the spin of the ball and the wheel.
Casinos will do their best to prevent (1) from happening, but they can’t do anything about (2). The reason why they can’t prevent (2) from happening is because bets are allowed to be placed after the wheel has started spinning. This means you can observe the motion of the ball and the wheel before placing a wager.
INDEX
The winners
Use physics to beat roulette
Look for a slant
History of scientific roulette
Strategies for both sides
The model
The completely flat table
The tilted table
People who have (successfully) tried to cheat and win
History is littered with people trying to squeeze money out of casinos. Here is a brief overview of a few that stand out.
- In 1873, an English mechanic and amateur mathematician who went by the name of Jagger carefully observed six roulette wheels at the Monte Carlo casino. He and his assistants logged the outcome of the each spin of the wheel for five weeks. Analysis of their data showed that each wheel had a unique bias due to factory imperfections which Jagger was quick to exploit. According to some sources, Jagger walked away with £65,000.
- In his daydreams about the nature of chance, Henri Poincaré used a slightly different version of a roulette wheel to show how sensitivity to initial conditions can be used to figure out the ultimate resting state of the wheel. Aside: sensitivity to initial conditions forms a cornerstone of modern chaos theory.
- Three gamblers who were arrested for hiding a laser scanner in their smartphones to predict where the roulette ball would most likely stop (based on the laser’s estimation of the ball’s velocity and position). Luckily for the gamblers (and not for the casino), they were released without any charges and were allowed to keep their £1.3 million winnings. The laser from the smart phone was linked to a computer that was able to make calculations fast enough for the three to make their bets before the dealer said, “No more bets.” The work of Small and Tse are extremely similar to this case.
Use physics to beat roulette
If you want to beat the house at roulette, it helps to think like a physicist. A simple model of the motion of a roulette wheel and ball, based on physics principles and confirmed by experiments on an actual wheel, has revealed two ways of overcoming the usual odds against roulette players.
The key, the modelers found, is knowing the precise location of the ball and the relative speeds of the ball and wheel when the croupier — the casino worker in charge of the game — sets the wheel in motion and releases the ball. Before going further it is good to have a basic understanding of the game.
| In this horizontal view you can see and understand the complex nature of the roulette track and wheel. |
“Knowing the initial conditions allows you to beat the odds,” said Michael Small, a statistician at the University of Western Australia in Perth, who carried out the study with Chi Kong Tse of Hong Kong Polytechnic University. “In some cases you can beat them quite significantly” according to their paper posted in the journal of chaos.
The simpler method the pair tested involves careful observation and recording of the initial conditions by an individual or team of players. In experiments on a roulette wheel in a laboratory, the method produced predicted earnings of almost 20 percent instead of the expected loss of about 2.7 percent for a European-style wheel. In U.S. casinos, the odds tilt further in the house’s favor because the wheel contains one extra space.
The other approach, using a digital camera mounted above the wheel to obtain the same data, provided better predictions. But for gamblers it presents the obvious problem of how to conceal the equipment in a security-conscious casino.
Look for a slant
And yet another factor increased the chances of beating the house even further. The scientists report that “a very slight slant in the roulette table, could … substantially enhance returns”
Small and Tse used high-school calculus and physics — specifically, the branch known as classical mechanics — to develop their model. They wrote down equations to predict the path the ball would take once the croupier releases it.
“We extrapolate that prediction to the point where the ball hits one of the deflectors — the raised bumps in the wheel’s rim that are added to increase the random bouncing of the ball,” Small explained. “Then we make a guess as to what portion of the wheel the ball is likely to land in.”
The pair tested their model on a standard casino roulette wheel installed in Tse’s laboratory. Small recorded on a computer the times at which the ball and a specific part of the roulette wheel passed a fixed point on the frame supporting the wheel.
“You basically press a button when the ball passes a certain point and then use that timing to make a prediction,” Small said. Predicting the half of the wheel in which the ball would settle would allow a gambler to bet on a combination of numbers with some confidence.
In 22 trials, Small and Tse predicted the correct half 13 times. Overall that would have earned them 18 percent profit on a theoretical stake, they report. “It is clear that in principle one should be able to make some predictions, given sufficient information,” said Holger Dullin of the University of Sydney in Australia. “The paper by Small and Tse did a good analysis.”
History of scientific roulette
The concept of using scientific understanding to beat the house isn’t new. In the late 1970s the “Eudaemons” a group of physics postgraduates, used theoretical insights and a rudimentary computer concealed in a shoe to win at roulette in Nevada in the 1970s. But since they didn’t publish their research, nobody outside their team knows the details of how they did it.
On the heels of this new research, however, J. Doyne Farmer, a group member who is now a professor of mathematics at Oxford, has written a report on the exploit that he plans to submit for publication.
“Small and Tse get some aspects of roulette prediction right,” Farmer said. “I can’t say whether their system would work, but I’m sure it is not as good as ours.”
Small and Tse extended their research by taking advantage of modern technology. They mounted a digital camera directly above their roulette wheel to obtain better measurements of the physical parameters. In 700 trials, they confirmed the validity of their model and identified certain numbers on the wheel in which the ball settled preferentially.
| The Eudaemons roulette system |
Strategies for both sides
The study suggests strategies for both sides of the roulette wheel.
“If you wish to beat the house, look for a wheel for which the ball drops only from one side of the rim — that is, a crooked table,” Small said. “Prediction becomes substantially simpler and more reliable.”
However, Small warned that roulette “is a game of chance. Even if the odds are in your favor, there is still a probability of losing, and losing big. In the long run you would come out ahead but you may first need very deep pockets.”
And Small also has some advice for casino owners. “Train the croupiers to spin the ball when they release it, and make sure that the tables are level and the air conditioning is working,” Small said, to allow for any influence of air resistance. He insists that his interest in gambling is purely theoretical. He has broken even in casinos by refusing to gamble there. “On one occasion I lost $20 on cocktails,” Small recalled. “And on another I gained $20, which I found on the floor.”
The model
Let’s use polar coordinates to describe the position of the ball, since we are on a wheel. We normally use Cartesian coordinates – the x-y plane – but due to the symmetry and naturally circular state of our system, polar coordinates are more intuitive. Polar coordinates describe location in space in terms of the distance from the origin  and angle measurement
and angle measurement 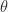 . The picture below describes the transformation from Cartesian to polar coordinates.
. The picture below describes the transformation from Cartesian to polar coordinates.
| Roulette wheel coordinates |
The authors model the ball as a single point, so its position in  can vary between
can vary between ![[0, r_{rim}] [0, r_{rim}]](/wp-content/uploads/2016/04/win-roulette-physics-scientific-prediction-im-4.jpg) , where
, where 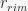 represents the farthest point from the middle of the wheel that the ball can be – the very edge of the wheel. Similarly,
represents the farthest point from the middle of the wheel that the ball can be – the very edge of the wheel. Similarly, 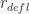 is the radial distance to the location of the metal deflectors on the fixed part of the wheel (stator).
is the radial distance to the location of the metal deflectors on the fixed part of the wheel (stator). 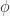 is the angle of rotation of the inner wheel.
is the angle of rotation of the inner wheel.
| Roulette wheel and ball physics diagram |
The physics diagram above also shows a free-body diagram of the forces acting on the ball as it travels on the roulette wheel.  is the mass of the ball. The angle
is the mass of the ball. The angle  is the angle of incline of the stator, and
is the angle of incline of the stator, and 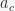 is the radial acceleration of the ball. Obviously,
is the radial acceleration of the ball. Obviously, 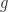 is gravity. The authors assume that the deflectors are evenly distributed around the stator at constant radius
is gravity. The authors assume that the deflectors are evenly distributed around the stator at constant radius 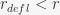 . In terms of a derivative, this means
. In terms of a derivative, this means 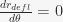 . There are going to be two models here: one model with a completely horizontal table and one model with a tilted surface. Comparing the two results shows how critical it is for the roulette wheel to be on a totally flat surface.
. There are going to be two models here: one model with a completely horizontal table and one model with a tilted surface. Comparing the two results shows how critical it is for the roulette wheel to be on a totally flat surface.
The completely flat table
The point in time 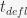 we are interested in is when
we are interested in is when 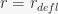 . In other words, we are looking for the time when the ball settles down in a pocket. Before the ball settles down, it will pass through four distinct states:
. In other words, we are looking for the time when the ball settles down in a pocket. Before the ball settles down, it will pass through four distinct states:
- Sufficient momentum to remain on the rim
- While on the rim,
 is constant, and the ball has a varying angular velocity
is constant, and the ball has a varying angular velocity  .
.  decays only due to a constant rolling friction.
decays only due to a constant rolling friction.
- While on the rim,
- Insufficient momentum; leaves the rim
- The ball leaves the rim at the point where its velocity squared is:
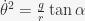 .
. - The time this happens is:
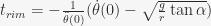
- The ball leaves the rim at the point where its velocity squared is:
- Moving freely on the stator
- Due to the force of gravity and the centripetal force, the ball’s radial position decreases. Integrating this differential equation reveals the ball’s position:

- As it turns out, for a level table, the time spent from leaving the rim of the wheel (1) until the ball is about to hit the deflectors (4) is fairly consistent because the ball leaves the stator with exactly the same velocity
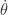 each time. Thus, it is possible to estimate the position of the ball without having to integrate the equation above by using tabulated numbers.
each time. Thus, it is possible to estimate the position of the ball without having to integrate the equation above by using tabulated numbers.
- Due to the force of gravity and the centripetal force, the ball’s radial position decreases. Integrating this differential equation reveals the ball’s position:
- Settling into a pocket
- The instantaneous angular deflection of the ball:
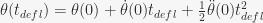
- The instantaneous angular deflection of the wheel:
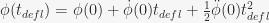
- The angular location on the wheel where the ball strikes a deflector:
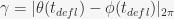 . Here,
. Here, 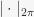 represents modulo
represents modulo 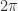 . A modulo operation returns the remainder after division of two numbers (e.g., 5 mod 4 = 1, 9 mod 10 = 9, -2 mod 3 = 1, …)
. A modulo operation returns the remainder after division of two numbers (e.g., 5 mod 4 = 1, 9 mod 10 = 9, -2 mod 3 = 1, …)
- The instantaneous angular deflection of the ball:
The tilted table
- Due to the change in the position of the wheel, it now has new equilibrium points. As a result, its angular velocity changes. Now,
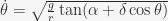
- The intersection of the above equation and this one will be the point the ball leaves the rim:
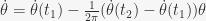
- For a tilted roulette wheel, the ball will favor one half of a wheel more than the other.
- A tilt of about 0.2 degrees is more than sufficient to bias the wheel.
After presenting these mathematical models for the motion of the wheel and the ball, the authors delve into some pretty lengthy and intense numerical simulations that support their model. They examine the sensitivity of their model to parameter uncertainty to see what sort of changes casinos may have to make to their roulette tables in order for the house to have a natural advantage (good news for the casinos; it’s only minor adjustments). The authors also realize that the game is truly predictable with some degree of certainty (good news for gamblers; this is a relatively honest game).